In this article we will delve into the probability of outcomes for blackjack to determine the best way to play in order to have an optimal outcome. To do so, we will calculate and compare the expected value of possible actions, taking the one with the largest outcome.
Expected Values: The expected value of a particular action is really the average value of all outcomes if you were to repeat the trial, in this case the hand and bet, an infinite number of times. While no one can play an infinite number of hands, after a few hundred you would get close. To get it exact, or close enough, we will calculate the probability of outcomes for each hand and use a standard bet of $100 (because hey, it’s fake money so we can be high rollers). With our $100 bet, an expected value of $10 would mean that on average we make $10 for every hand we play in this manner. So, play 100 hands with an expected value of $10 and you should expect to win $1,000! You probably won’t win exactly that much, but close, maybe a little more, maybe a little less. Conversely, play 100 hands with an expected value of -$10 and should expect to lose $1,000.
Our game assumptions:
Dealer stands on soft 17: This makes the computation easier. In season 2 we can change this, but we do know that a dealer hitting on soft 17 decreases your odds of winning slightly, that means that the your expected value is slightly lower than stated playing that type of table.
Early Surrender: This is easy, the outcome is guaranteed with this choice, it’s 50% of your bet. When playing a table that offers this option, if there’s no way to get an expected value greater than -$50 then you should take it. (Hint: there are a few times where this is true)
Max cards: With every dealer hand, there is a small chance that it takes several cards to finish the hand. Our calculations only account for 5 cards. We do share the probability of the dealer needing more cards but because the count is so low and split between both wins and losses, the impact to expected value is negligible.
Number of Decks: We have chosen 8 decks for this computation. Note that while this assumes the deck is full, you can only change your odds if you know exactly what has already been dealt. We assume you haven’t counted the cards in any way. Maybe we can explore that in season 3!
Hard 15’s only: Having a soft 15 changes things dramatically so we will deal with soft hands another time.
Our 15’s are calculated for 10-5, but the numbers don’t change much regardless of the way you get 15, whether it’s with 9-6 or 5-5-5. Regardless of how you get to 15, soft 15 excluded, the same rules apply, though the expected values change a little (mostly for the worse).
How often are you dealt a 15? Including just the 3 possible 2 card hands, you can expect this unlucky hand about 7.12% of the time. That means, if you plan to play 1,000 hands, you should expect this about 68 to 74 times.
15 vs 2:
You’re sitting on 15 and staring at the dealers 2. You know the dealer must take a card. What are the odds they bust? That would be 36.28%. If you choose to stand, this is your only hope. If you take a card you might be able to beat the dealer, but taking just 1 card gives you a 53.85% chance of busting, and you lose, regardless of what the dealers does. Here is a break down of what happens if you draw a card:
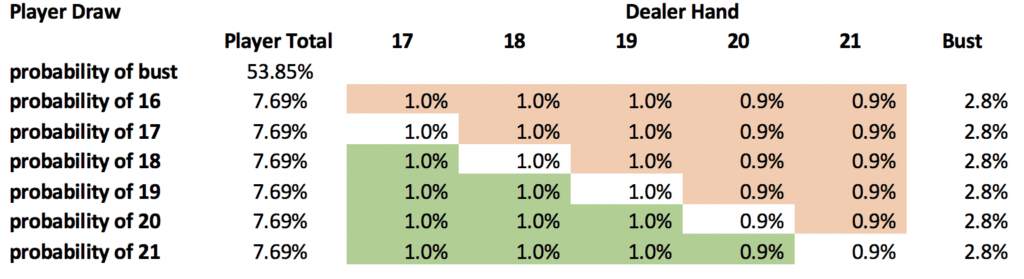
So, even if you take a card the dealer will still win, fairly often. In total here are the outcomes of your two choices (more cards means the dealer did not get to 17 with 5 cards):
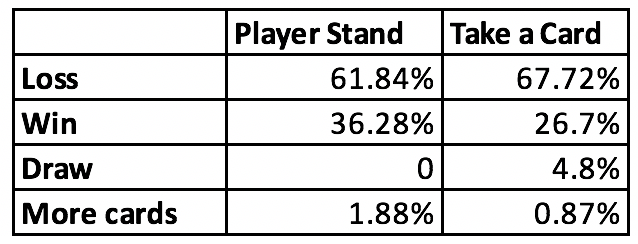
By multiplying the probability of each outcome by the $100 bet and totaling those values we come to an expected value.
If you stand, the expected value is -$25.56. That is on average you will lose $25.56. If you hit, the expected value is -$41.07. That is, on average you will lose $41.07.
So, no good options here. You will lose either way, but the less negative outcome is to stand. And if you’re thinking, what about surrender, should that be available, the expected value of that is -$50. Definitely don’t do that.
Dealer showing 3,4,5, or 6
For each of these hands you do a little better, but the expected value is always negative. And in each case, you best move is to stand. For each hand, the expected value of the standing in $15 or more higher than if you hit. The table below has a complete set of odds and expected values for each hand.
Dealer showing 7,8, or 9
Here’s where the news starts to get bad, as if it wasn’t already. Because of the high likelihood that the dealer will make a hand, the expected value of standing drops to negative $47.68 against a 7 and down to negative $54.32 against a 9. (Really bad). This means that even though you have over a 50% chance of busting, by taking a card you do improve you odds of winning, and the expected value. All the way up to a negative $37.52 against a 7 or negative $47.46 against a 9. Still better than surrendering, but not much.
Dealer Showing 10
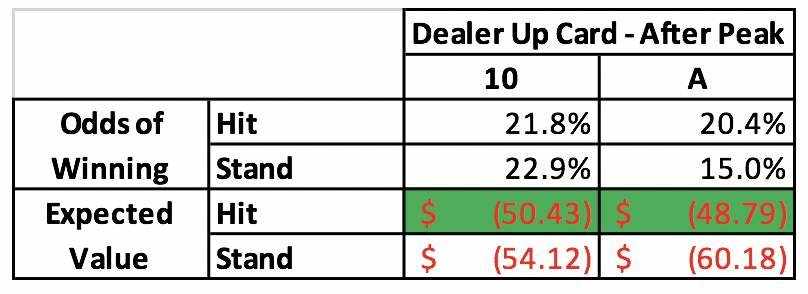
Just hand over you bet. Ok, it’s not that bad, but close. Including the dealer blackjack, where you don’t really have a choice, the expected value of the standing, the best move, is negative $53.66. After the peak, assuming the dealer doesn’t have Blackjack, the best play is still to hit, with the expected value climbing to negative $50.43. That means a surrender is a good play here, but just barely.
Dealer showing Ace
First, note that the odds of the dealer getting black jack here is 30.8%, so insurance isn’t a good bet. That also means that 30% of hands will end without you making a decision. Should you get to make a decision, taking a card gives you an expected value of negative $48.79. still not a good had but it’s you best option.
Here’s a full summary of the odds and expected values against a $100 bet:

The Takeaway
Getting a 15 sucks. Regardless of what the dealer has, you will lose more than you win on these hands. But the good news is that with a smart play, you can minimize your losses and look for better hands to bet on.
Click here to read our online poker site reviews.
